一、正交实验设计过程

采用正交实验设计选择实验方案的过程比较复杂，为了简化设计过程，日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格，称为正交表。

最简单的正交表是

，含意如下：“L”代表正交表；L 下角的数字“4”表示有 4 横行，简称行，即要做四次试验；括号内的指数“3”表示有3 纵列，简称列，即最多允许安排的属性是3 个；括号内的数“2”表示表的主要部分只有2 种数字，即每个属性有两种水平1与2。正交表的特点是其安排的试验方法具有均衡搭配特性。也就是说，3个属性，每个属性有2个水平的选择实验采用全因子设计需要23=8个备选方案，而采用正交设计只需要4个。当然这是非常简单，差异并不明显design-expert能用于正交实验数据分析吗，但是如果属性和水平都比较大，二者的差异就会非常明显，显然能够大大减少工作量。因而正交实验设计在包括选择实验在内的很多领域研究中已经得到广泛应用。正交设计的数量可以用以下公式来计算：

n=c×s-c+1

其中n为正交设计的数量，即正交表中的行，c为属性的数量，即正交表中的列，s为属性水平的数量。

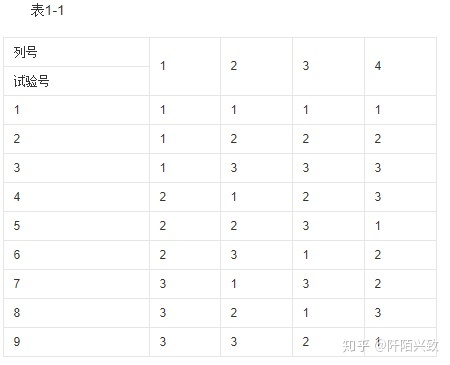
正交表例如

，表1-1， 它表示需作9次实验，最多可观察4个属性，每个属性均为3水平。根据正交表的数据结构看出，正交表是一个n行c列的表，其中第j列由数码1，2，…

组成design-expert能用于正交实验数据分析吗，这些数码均各出现n/

次，例如表1-1中，第二列的数码个数为3，S=3 ，即由1、2、3组成，各数码均出现3次。

如果我们所做的选择实验是4个属性，每个属性3个水平，我们可以将每个属性水平进行编号，然后按照表1-1中的编号代入属性水平，每一行就是一个备选方案，即被调查者面临的产品组合，共构建了8个。

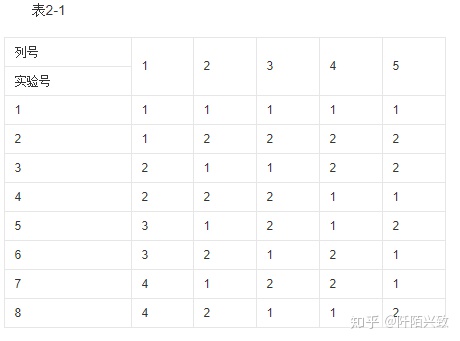
一个正交表中也可以各列的水平数不相等，我们称它为混合型正交表，如

，表2-1 ，此表的5列中，有1列为4水平，4列为2水平。n=4+4×2-5+1=8

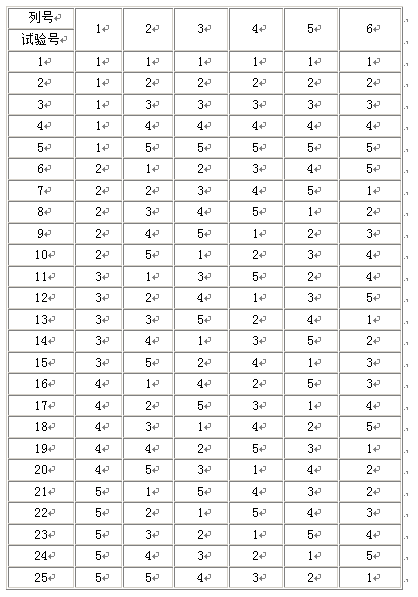
二、正交实验设计的性质：

（1）每一列中，不同的数字出现的次数相等。例如在两水平正交表中，任何一列都有数码“1”与“2”，且任何一列中它们出现的次数是相等的；如在三水平正交表中，任何一列都有“1”、“2”、“3”，且在任一列的出现数均相等。

（2）任意两列中数字的排列方式齐全而且均衡。例如在两水平正交表中，任何两列（同一横行内）有序对子共有4种：（1，1）、（1，2）、（2，1）、（2，2）。每种对数出现次数相等。在三水平情况下，任何两列（同一横行内）有

来源【首席数据官】，更多内容/合作请关注「辉声辉语」公众号，送10G营销资料！