数据可视化分析的好处

1

在不歪曲事实的情况下传达正确和必要的信息。

2

设计简单。

3

美学支持信息而不是掩盖信息。

4

没有超载信息。

关联图表用于可视化2个或更多变量之间的关系。 也就是说，一个变量如何相对于另一个变化。

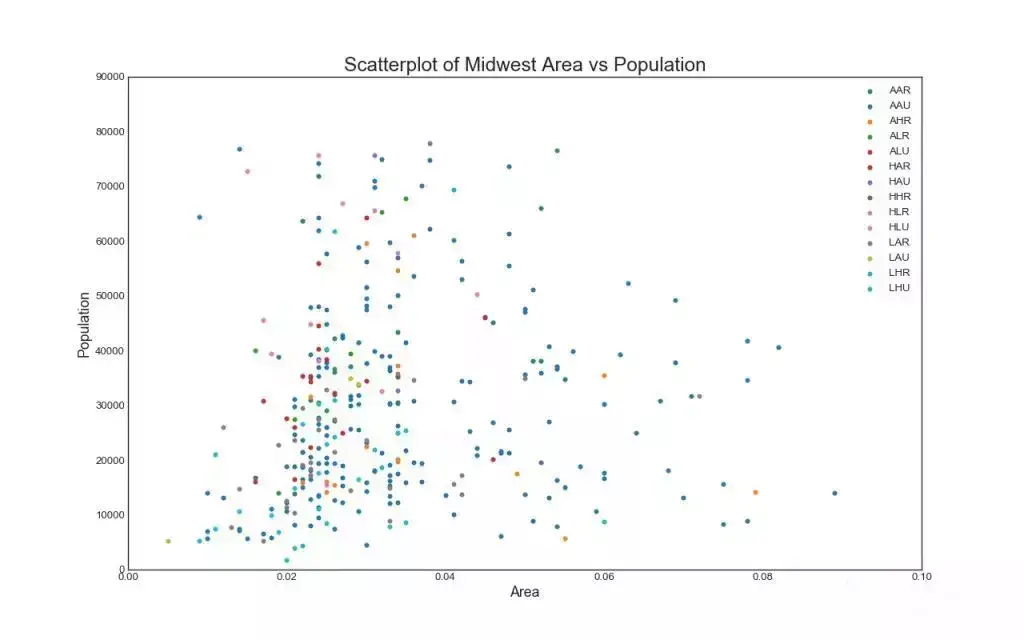
1. 散点图(Scatter plot)

散点图是用于研究两个变量之间关系的经典的和基本的图表。 如果数据中有多个组，则可能需要以不同颜色可视化每个组。

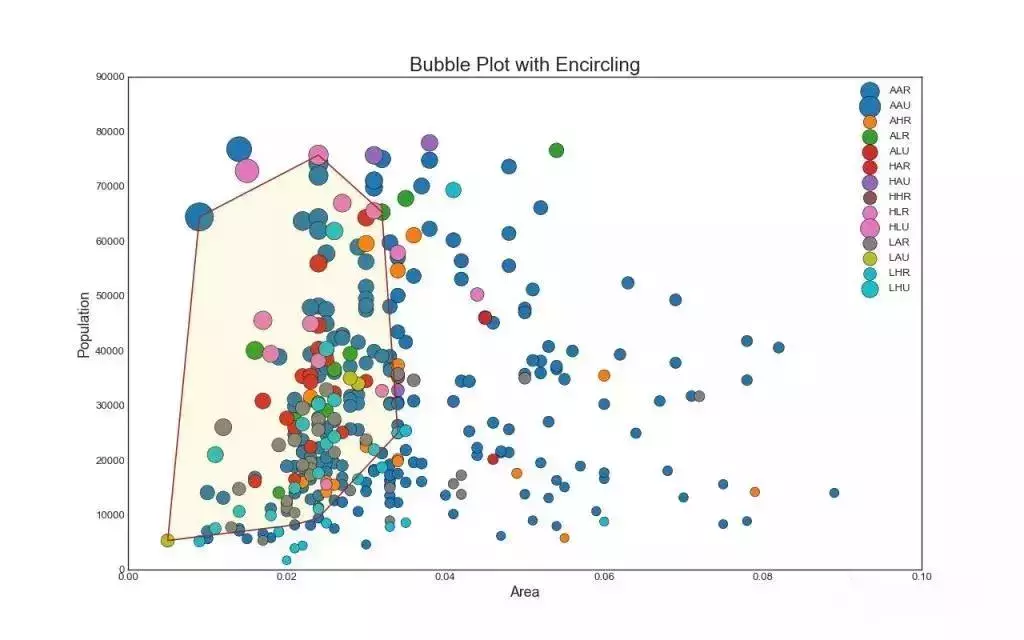
2. 带边界的气泡图(Bubble plot with Encircling)

有时，您希望在边界内显示一组点以强调其重要性。

3. 带线性回归最佳拟合线的散点图 (Scatter plot with linear regression line of best fit)

如果你想了解两个变量如何相互改变，那么最佳拟合线就是常用的方法。 下图显示了数据中各组之间最佳拟合线的差异。

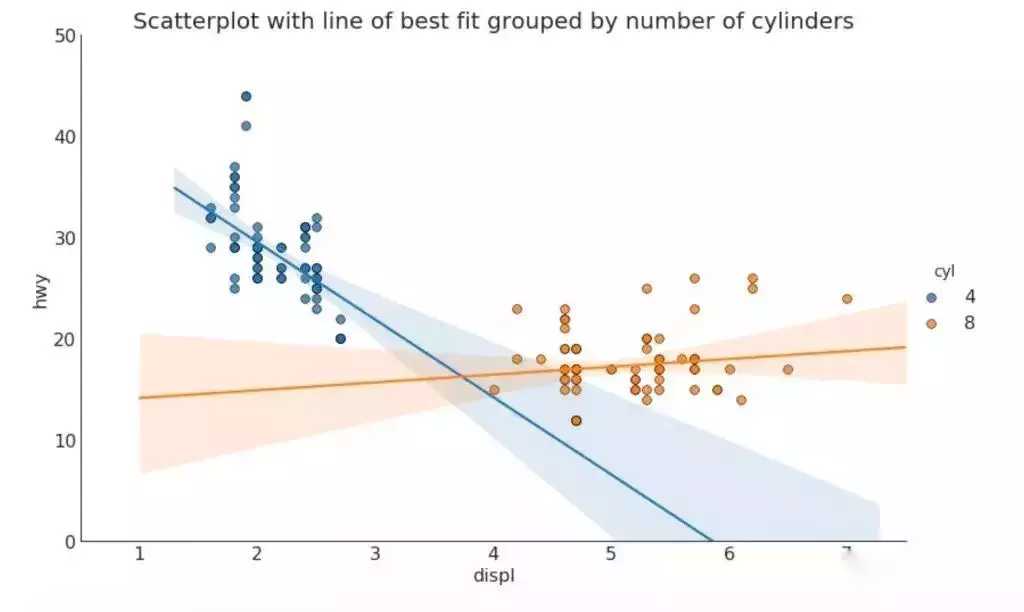
针对每列绘制线性回归线：

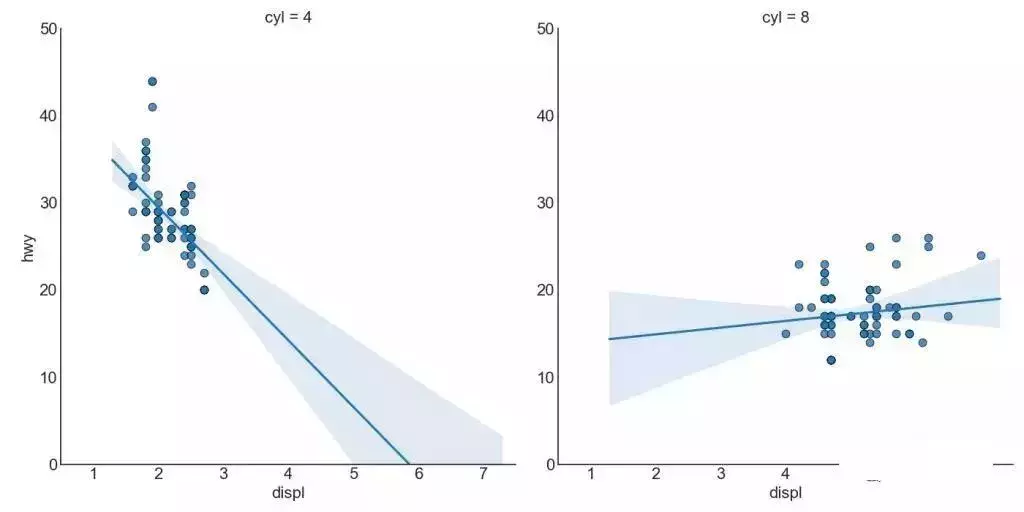
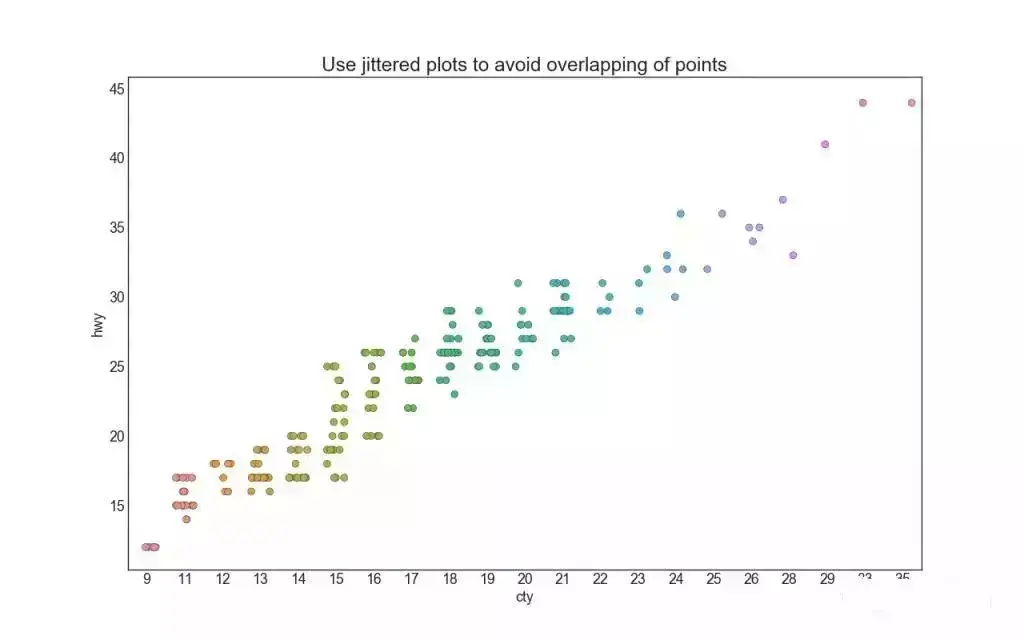
4. 抖动图 (Jittering with stripplot)

通常，多个数据点具有完全相同的 X 和 Y 值。 结果，多个点绘制会重叠并隐藏。 为避免这种情况，请将数据点稍微抖动，以便您可以直观地看到它们。

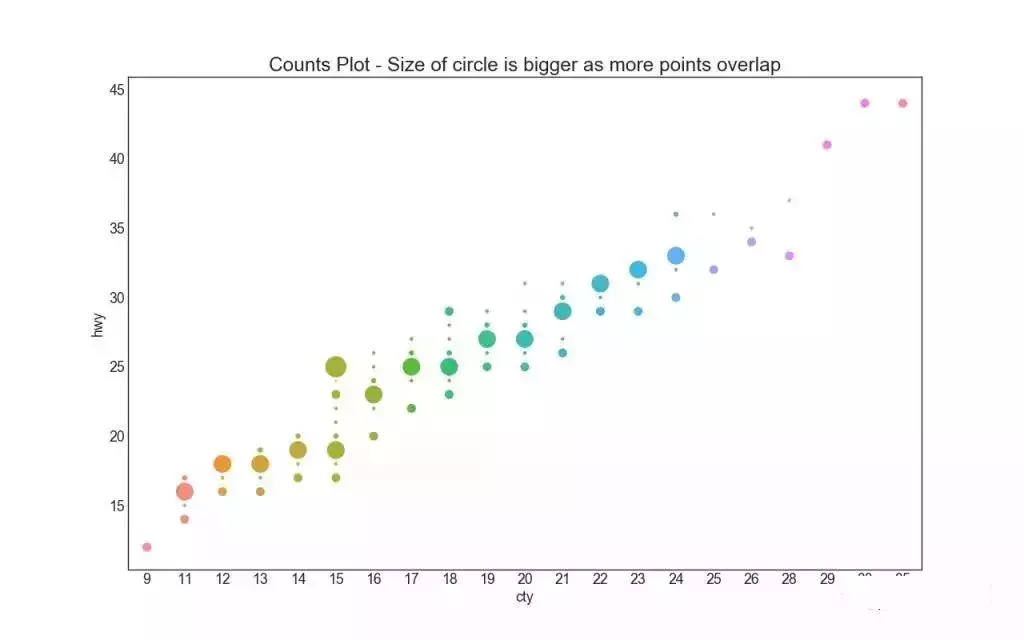
5. 计数图 (Counts Plot)

避免点重叠问题的另一个选择是增加点的大小，这取决于该点中有多少点。 因此，点的大小越大，其周围的点的集中度越高。

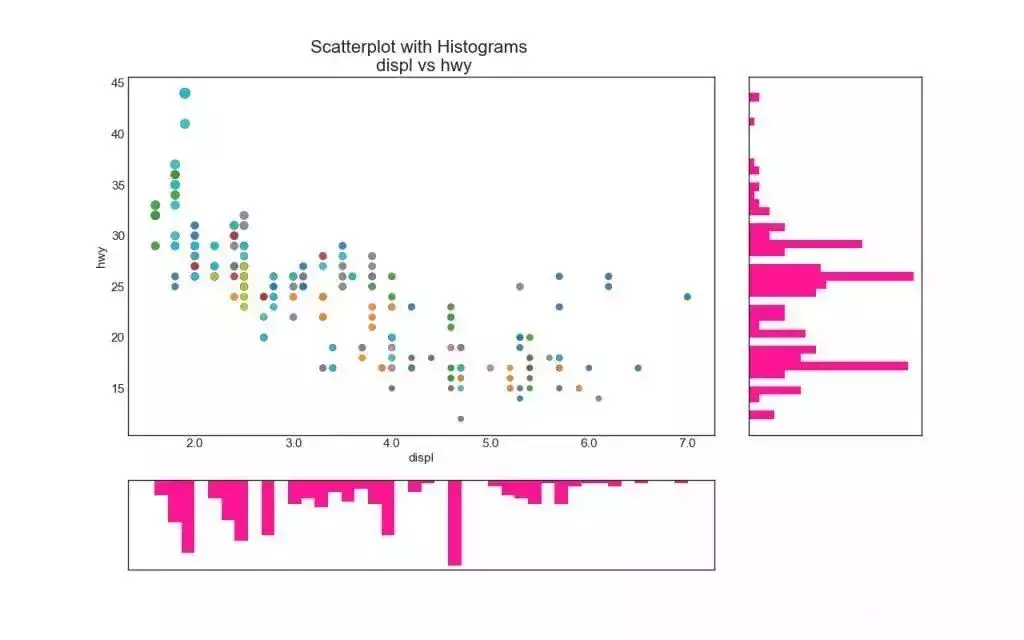
6. 边缘直方图 (Marginal Histogram)

边缘直方图具有沿 X 和 Y 轴变量的直方图。 这用于可视化 X 和 Y 之间的关系以及单独的 X 和 Y 的单变量分布。 这种图经常用于探索性数据分析(EDA)。

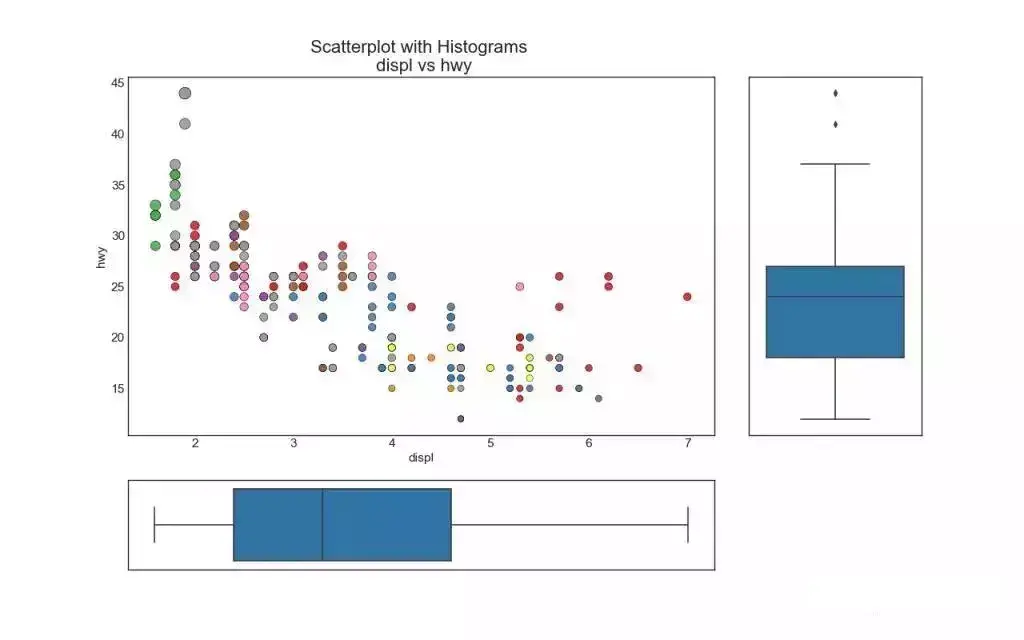
7. 边缘箱形图 (Marginal Boxplot)

边缘箱图与边缘直方图具有相似的用途。 然而，箱线图有助于精确定位 X 和 Y 的中位数、第25和第75百分位数。

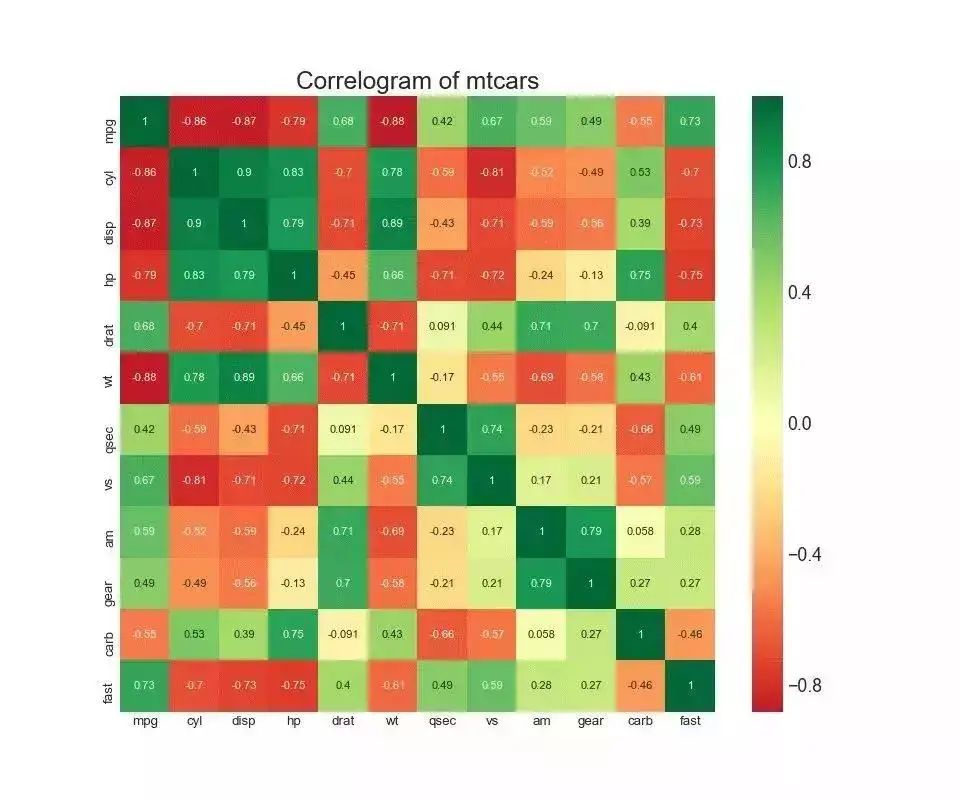
8. 相关图 (Correllogram)

相关图用于直观地查看给定数据框(或二维数组)中所有可能的数值变量对之间的相关度量。

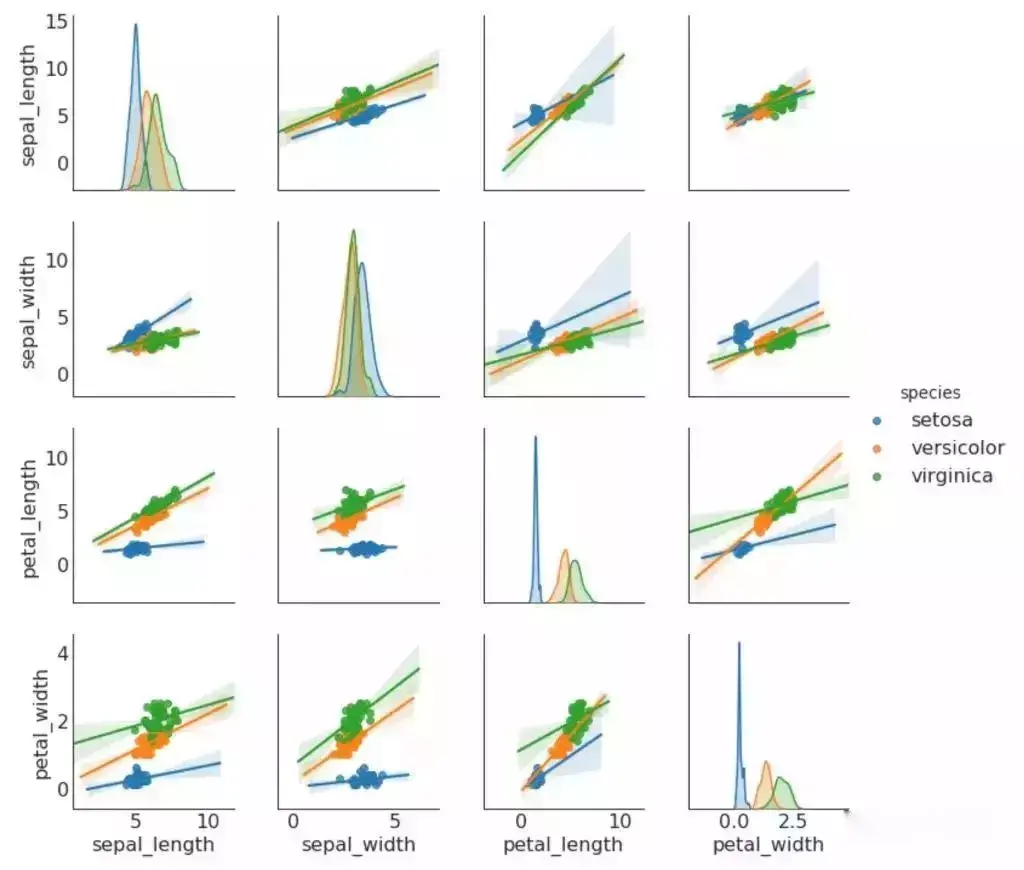
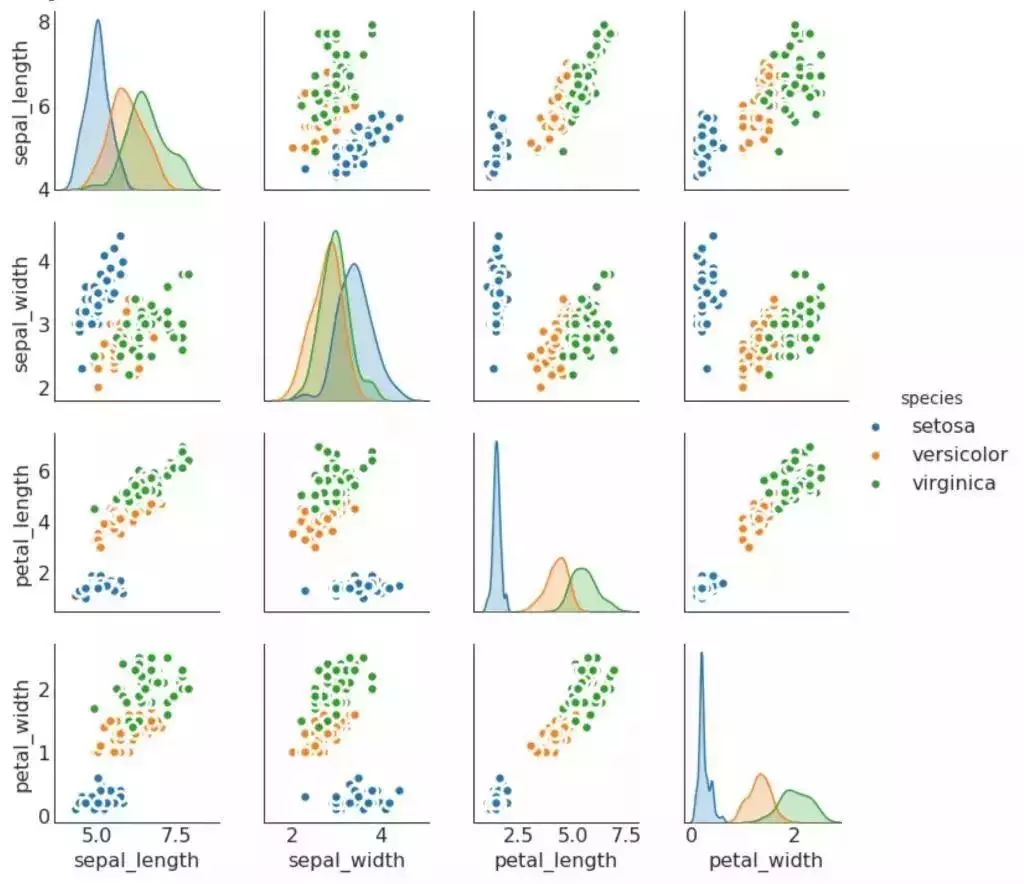
9. 矩阵图 (Pairwise Plot)

矩阵图是探索性分析中的最爱，用于理解所有可能的数值变量对之间的关系。 它是双变量分析的必备工具。

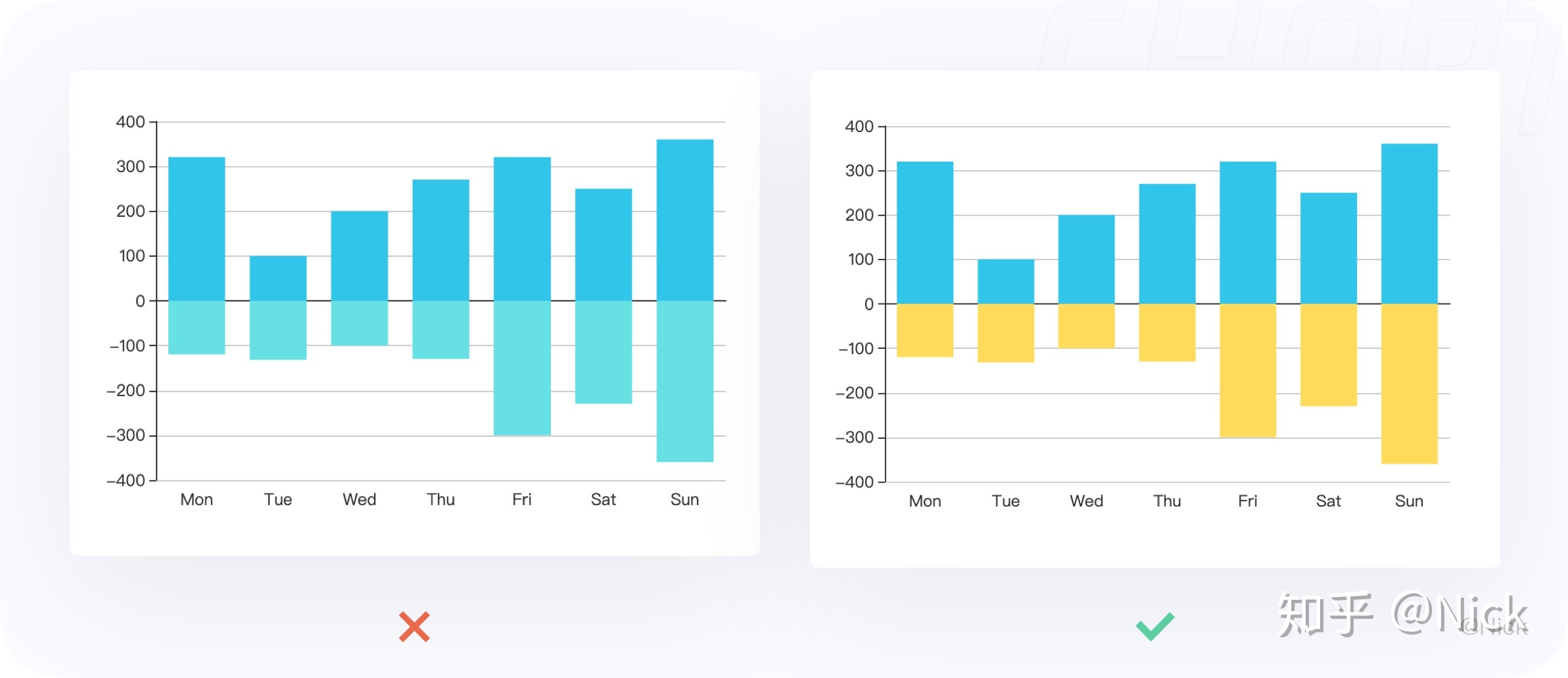
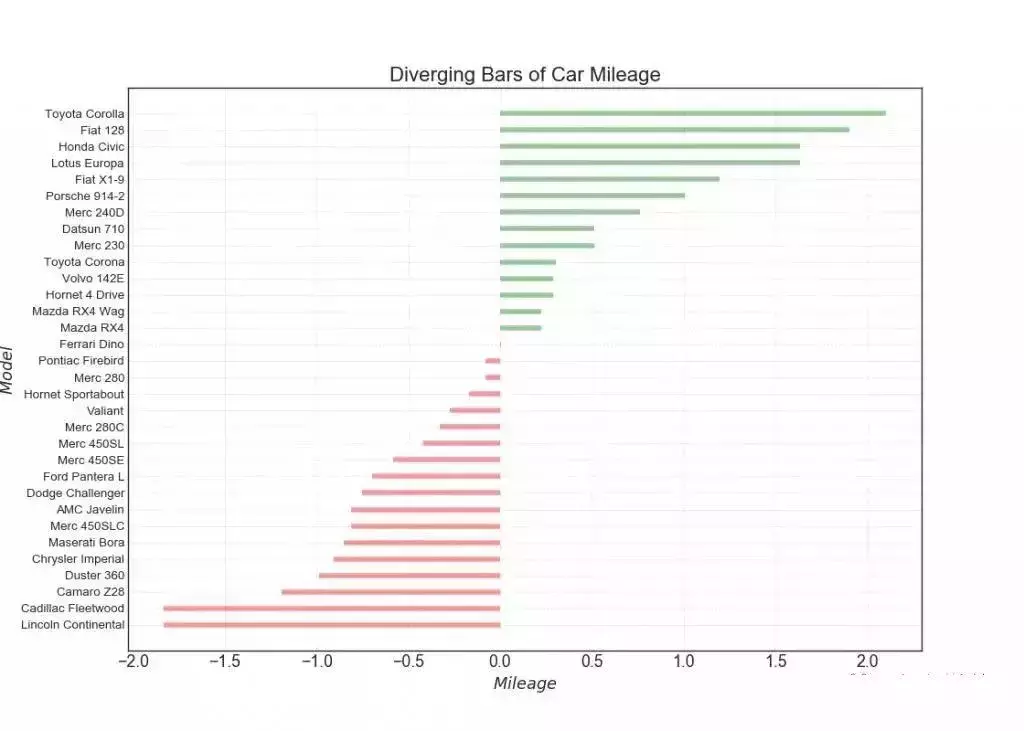
10. 发散型条形图 (Diverging Bars)

如果您想根据单个指标查看项目的变化情况，并可视化此差异的顺序和数量，那么散型条形图 (Diverging Bars) 是一个很好的工具。它有助于快速区分数据中组的性能，并且非常直观，并且可以立即传达这一点。

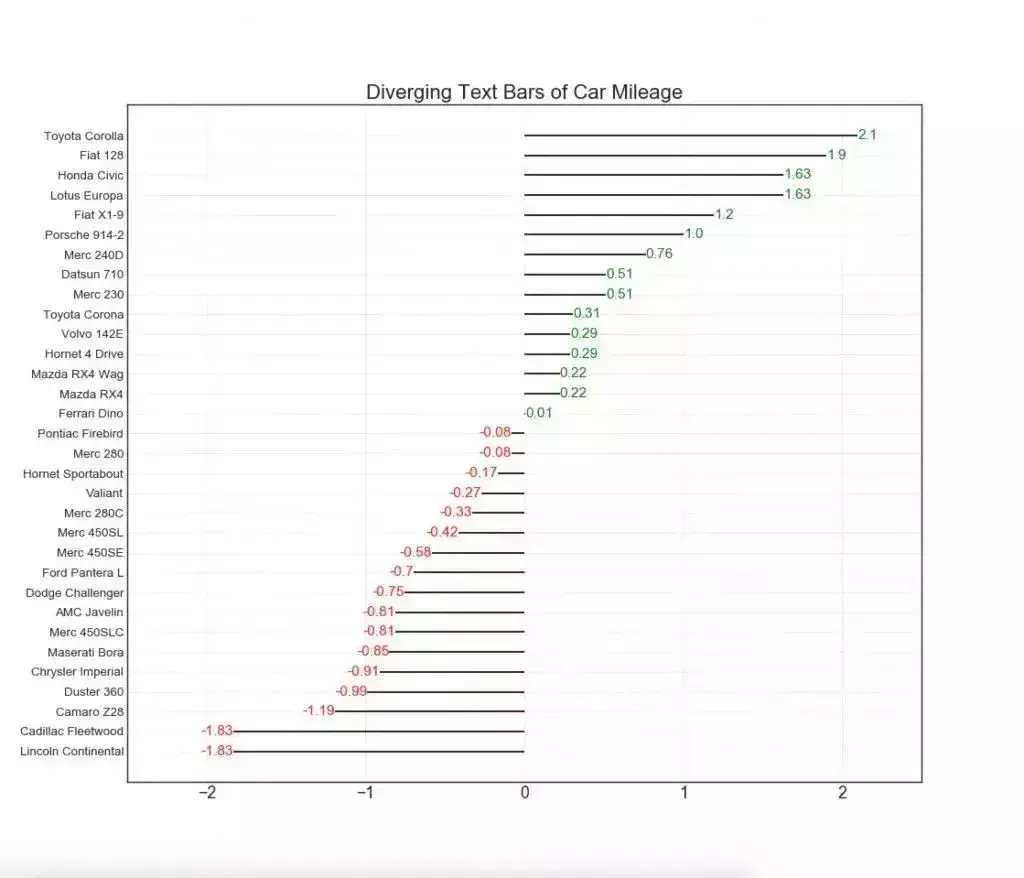
11. 发散型文本 (Diverging Texts)

发散型文本 (Diverging Texts)与发散型条形图 (Diverging Bars)相似数据可视化分析，如果你想以一种漂亮和可呈现的方式显示图表中每个项目的价值，就可以使用这种方法。

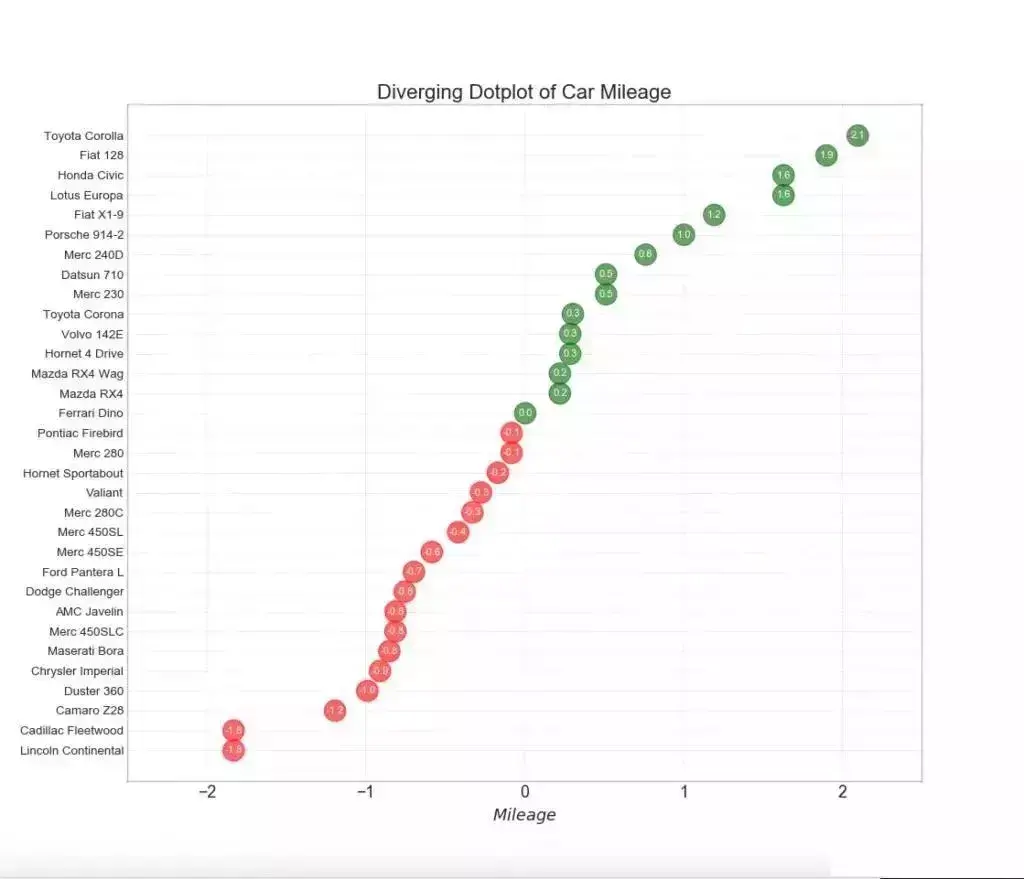
12. 发散型包点图 (Diverging Dot Plot)

发散型包点图 (Diverging Dot Plot)也类似于发散型条形图 (Diverging Bars)。 然而，与发散型条形图 (Diverging Bars)相比，条的缺失减少了组之间的对比度和差异。

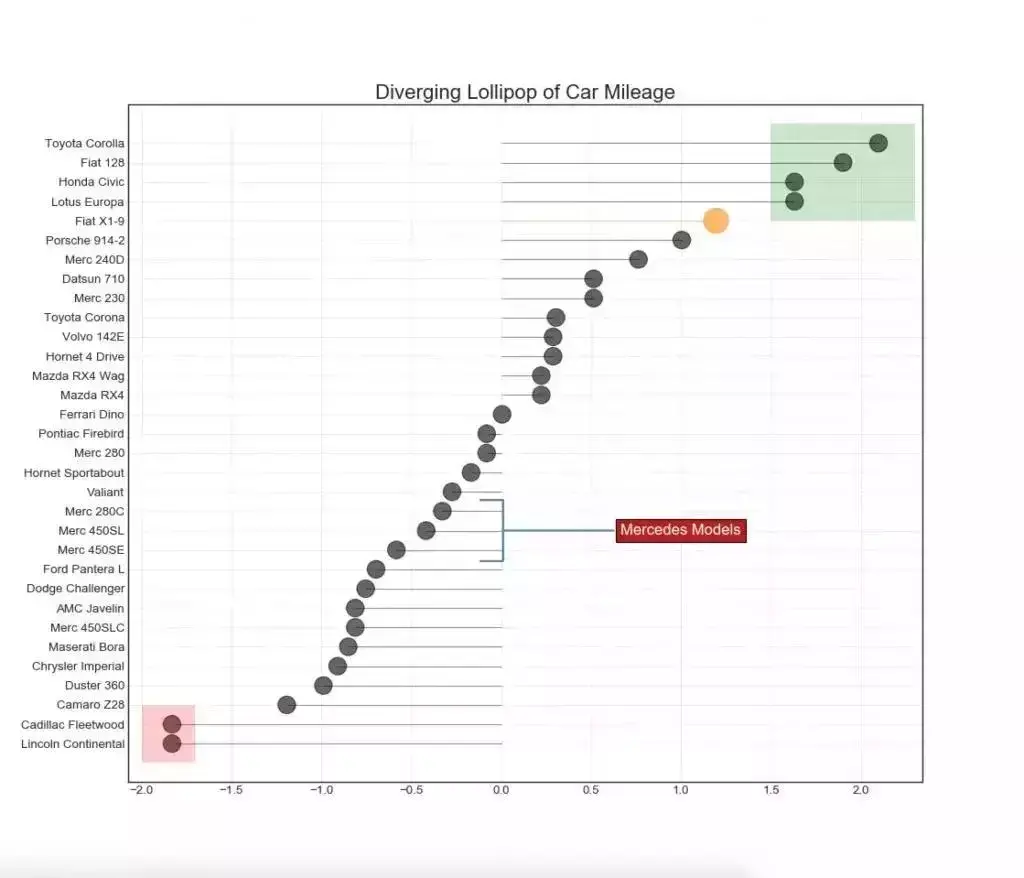
13. 带标记的发散型棒棒糖图 (Diverging Lollipop Chart with Markers)

带标记的棒棒糖图通过强调您想要引起注意的任何重要数据点并在图表中适当地给出推理，提供了一种对差异进行可视化的灵活方式。

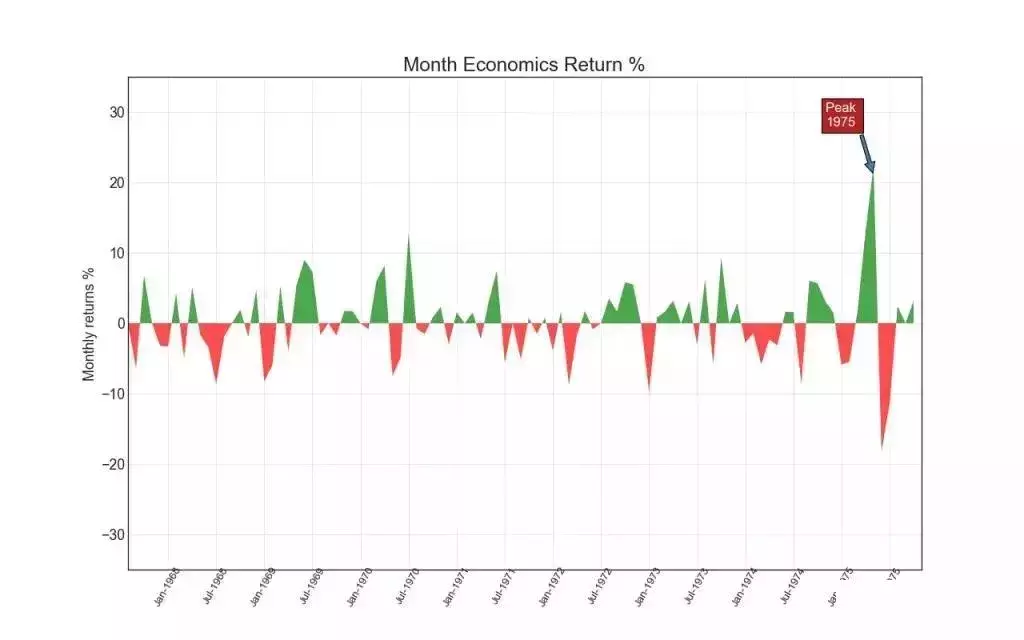
14. 面积图 (Area Chart)

通过对轴和线之间的区域进行着色，面积图不仅强调峰和谷，而且还强调高点和低点的持续时间。 高点持续时间越长，线下面积越大。

来源【首席数据官】，更多内容/合作请关注「辉声辉语」公众号，送10G营销资料！