时间序列数据趋势分析 Cox-Stuart、Mann_技术分析

时序数据趋势检测斜率法

原理:

斜率法的原理就是使用最小二乘等方法对时序数据进行拟合，然后根据拟合成的直线的斜率k判断序列的数据走势，当k>0时，则代表趋势上升；当k 优缺点:

优点是方法简单；缺点是要求趋势是线性的，当数去波动较大时无法准确拟合。

Cox-Stuart检验

原理

直接考虑数据的变化趋势监测数据分析，若数据有上升趋势，那么排在后面的数据的值要比排在前面的数据的值显著的大，反之，若数据有下降趋势，那么排在后面的数据的值要比排在前面的数据的值显著的小，利用前后两个时期不同数据的差值正负来判断数据总的变化趋势。

算法步骤

优缺点:

优点是不依赖趋势结构，可以快速判断趋势是否存在；缺点是未考虑数据的时序性，仅从符号检验来判断。

代码

动态血糖监测数据分析_苹果睡眠监测数据分析_监测数据分析

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author  : LaoChen
import numpy as np
import pandas as pd
import scipy.stats as stats
def cox_staut(list_c):
    lst=list_c.copy()
    n0=len(lst)
    if n0%2==1:
        del lst[int((n0-1)/2)]
    c=int(len(lst)/2)
    pos=neg=0
    for i in range(c):
        diff=lst[i+c]-lst[i]
        if diff>0:
            pos+=1
        elif diff0:
            neg+=1
        else:
            continue
    n1=pos+neg
    k=min(pos,neg)
    p=2*stats.binom.cdf(k,n1,0.5)
    print('fall:%i  rise:%i  p-value:%f'%(neg,pos,p))
cox_staut([206,223,235,264,229,217,188,204,182,230,223,227,242,238,207,208,
           216,233,233,274,234,227,221,214,226,228,235,237,243,240,231,210])

Mann-Kendall检验

原理

Mann-Kendall检验不需要样本遵循一定的分布，也不受少数异常值的干扰。在Mann-Kendall检验中，原假设H0为时间序列数据（X1，…,Xn),是n个独立的、随机变量同分布的样本；备择假设H1 是双边检验，对于所有的k，j≤n，且k≠j，Xk和Xj的分布是不相同的。若原假设是不可接受的，即在α置信水平上，时间序列数据存在明显的上升或下降趋势。对于统计量Z监测数据分析，大于0时是上升趋势；小于0时是下降趋势。

算法步骤

import math
from scipy.stats import norm, mstats
def mk_test(x, alpha=0.05):
    n = len(x)
    # calculate S
    s = 0
    for k in range(n-1):
        for j in range(k+1, n):
            s += np.sign(x[j] - x[k])
    # calculate the unique data
    unique_x, tp = np.unique(x, return_counts=True)
    g = len(unique_x)
    # calculate the var(s)
    if n == g:  # there is no tie
        var_s = (n*(n-1)*(2*n+5))/18
    else:  # there are some ties in data
        var_s = (n*(n-1)*(2*n+5) - np.sum(tp*(tp-1)*(2*tp+5)))/18
    if s > 0:
        z = (s - 1)/np.sqrt(var_s)
    elif s  0:
        z = (s + 1)/np.sqrt(var_s)
    else: # s == 0:
        z = 0
    # calculate the p_value
    p = 2*(1-norm.cdf(abs(z)))  # two tail test
    h = abs(z) > norm.ppf(1-alpha/2)
    if (z  0) and h:
        trend = 'decreasing'
    elif (z > 0) and h:
        trend = 'increasing'
    else:
        trend = 'no trend'
    return trend

在python中使用mann-Kendall，可以用scipy.stats.kendalltau，该函数返回两个值：tau-反映两个序列的相关性，接近1的值表示强烈的正相关，接近-1的值表示强烈的负相关；p_value：p值反映的是假设检验的双边p值，其零假设为无关联——即通常所谓的显著性水平，一般取p 稳定性检验滚动统计

平稳时间序列有两种定义：严平稳和宽平稳

严平稳顾名思义，是一种条件非常苛刻的平稳性，它要求序列随着时间的推移，其统计性质保持不变。对于任意的τ，其联合概率密度函数满足：

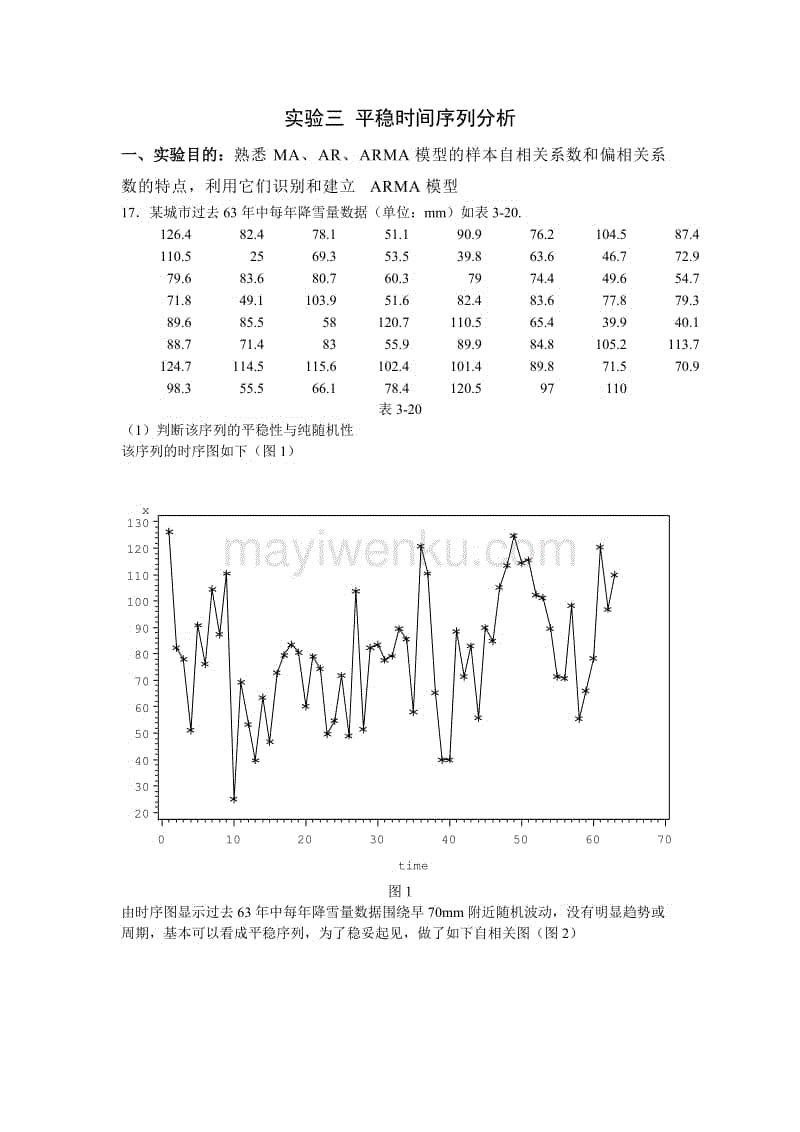
动态血糖监测数据分析_监测数据分析_苹果睡眠监测数据分析

严平稳的条件只是理论上的存在，现实中用得比较多的是宽平稳的条件。

宽平稳也叫弱平稳或者二阶平稳（均值和方差平稳），满足：

常数均值

常数方差

常数自协方差

from statsmodels.tsa.stattools import adfuller
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
 
# 移动平均图
def draw_trend(timeSeries, size):
    f = plt.figure(facecolor='white')
    # 对size个数据进行移动平均
    rol_mean = timeSeries.rolling(window=size).mean()
    # 对size个数据进行加权移动平均
    rol_weighted_mean = pd.ewma(timeSeries, span=size)
 
    timeSeries.plot(color='blue', label='Original'