t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。此外，t-SNE 是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。当我们想要对高维数据进行分类，又不清楚这个数据集有没有很好的可分性（即同类之间间隔小，异类之间间隔大），可以通过t-SNE投影到2维或者3维的空间中观察一下。如果在低维空间中具有可分性，则数据是可分的；如果在高维空间中不具有可分性，可能是数据不可分，也可能仅仅是因为不能投影到低维空间。t-SNE是由SNE(Stochastic Neighbor Embedding, SNE; Hinton and Roweis, 2002)发展而来。我们先介绍SNE的基本原理，之后再扩展到t-SNE。最后再看一下t-SNE的实现以及一些优化。

目录

SNE

基本原理

SNE是通过仿射(affinitie)变换将数据点映射到概率分布上，主要包括两个步骤：

我们看到t-SNE模型是非监督的降维，他跟kmeans等不同，他不能通过训练得到一些东西之后再用于其它数据（比如kmeans可以通过训练得到k个点，再用于其它数据集，而t-SNE只能单独的对数据做操作，也就是说他只有fit_transform，而没有fit操作）

SNE原理推导

SNE是先将欧几里得距离转换为条件概率来表达点与点之间的相似度。具体来说，给定一个N个高维的数据$x_1, … , x_N$（注意N不是维度）, t-SNE首先是计算概率$p_{ij}$，正比于$x_i$和$x_j$之间的相似度（这种概率是我们自主构建的），即：

$${p_ {j \mid i} = \frac{\exp(- \mid \mid x_i -x_j \mid \mid ^2 / (2 \sigma^2_i ))} {\sum_{k \neq i} \exp(- \mid \mid x_i – x_k \mid \mid ^2 / (2 \sigma^2_i))}}$$

这里的有一个参数是$\sigma_i$，对于不同的点$x_i$取值不一样，后续会讨论如何设置。此外设置$ p_{x \mid x}=0$,因为我们关注的是两两之间的相似度。

那对于低维度下的$y_i$，我们可以指定高斯分布为方差为$\frac{1}{\sqrt{2}}$，因此它们之间的相似度如下：

$${q_ {j \mid i} = \frac{\exp(- \mid \mid x_i -x_j \mid \mid ^2)} {\sum_{k \neq i} \exp(- \mid \mid x_i – x_k \mid \mid ^2)}}$$

同样，设定$ q_{i \mid i} = 0$.

如果降维的效果比较好，局部特征保留完整，那么$p_{i \mid j} = q_{i \mid j}$, 因此我们优化两个分布之间的距离-KL散度(Kullback-Leibler divergences)，那么目标函数(cost function)如下:

$$C = \sum_i KL(P_i \mid \mid Q_i) = \sum_i \sum_j p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}}$$

这里的$P_i$表示了给定点$x_i$下，其他所有数据点的条件概率分布。需要注意的是KL散度具有不对称性，在低维映射中不同的距离对应的惩罚权重是不同的，具体来说：距离较远的两个点来表达距离较近的两个点会产生更大的cost，相反，用较近的两个点来表达较远的两个点产生的cost相对较小(注意：类似于回归容易受异常值影响，但效果相反)。即用较小的$q_{j \mid i}=0.2$来建模较大的$ p_{j \mid i}=0.8$, $cost= p \log(\frac{p}{q})=1.11$，同样用较大的$q_{j \mid i}=0.8$来建模较大的$p_{j \mid i}=0.2$，$cost=-0.277$, 因此，SNE会倾向于保留数据中的局部特征。

了解了基本思路之后，你会怎么选择$\sigma$，固定初始化? 下面我们开始正式的推导SNE。首先不同的点具有不同的$\sigma_i$，$P_i$的熵(entropy)会随着$\sigma_i$的增加而增加。SNE使用困惑度(perplexity)的概念，用二分搜索的方式来寻找一个最佳的$\sigma$。其中困惑度指：$Perp(P_i) = 2^{H(P_i)}$。这里的$H(Pi)$是$P_i$的熵，即:

$$H(P_i) = -\sum_j p_{j \mid i} \log_2 p_{j \mid i}$$

困惑度可以解释为一个点附近的有效近邻点个数。SNE对困惑度的调整比较有鲁棒性，通常选择5-50之间，给定之后，使用二分搜索的方式寻找合适的$\sigma$。

那么核心问题是如何求解梯度了,目标函数等价于$\sum \sum – p log(q)$这个式子与softmax非常的类似，我们知道softmax的目标函数是$\sum -y \log p$，对应的梯度是$y−p$(注：这里的softmax中y表示label，p表示预估值)。 同样我们可以推导SNE的目标函数中的i在j下的条件概率情况的梯度是$2(p_{i \mid j}-q_{i \mid j})(y_i-y_j)$， 同样j在i下的条件概率的梯度是$2(p_{j \mid i}-q_{j \mid i})(y_i-y_j)$, 最后得到完整的梯度公式如下：

$$\frac{\delta C}{\delta y_i} = 2 \sum_j (p_{j \mid i} – q_{j \mid i} + p_{i \mid j} – q_{i \mid j})(y_i – y_j)$$

在初始化中，可以用较小的σ下的高斯分布来进行初始化。为了加速优化过程和避免陷入局部最优解高维数据可视化，梯度中需要使用一个相对较大的动量(momentum)。即参数更新中除了当前的梯度，还要引入之前的梯度累加的指数衰减项，如下：

$$Y^{(t)} = Y^{(t-1)} + \eta \frac{\delta C}{\delta Y} + \alpha(t)(Y^{(t-1)} – Y^{(t-2)})$$

这里的$Y^{(t)}$表示迭代t次的解，$\eta$表示学习速率, $\alpha(t)$表示迭代t次的动量。

此外，在初始优化的阶段，每次迭代中可以引入一些高斯噪声，之后像模拟退火一样逐渐减小该噪声，可以用来避免陷入局部最优解。因此，SNE在选择高斯噪声，以及学习速率，什么时候开始衰减，动量选择等等超参数上，需要跑多次优化才可以。

t-SNE

尽管SNE提供了很好的可视化方法，但是他很难优化，而且存在”crowding problem”(拥挤问题)。后续中，Hinton等人又提出了t-SNE的方法。与SNE不同，主要如下:

t-SNE在低维空间下使用更重长尾分布的t分布来避免crowding问题和优化问题。在这里，首先介绍一下对称版的SNE，之后介绍crowding问题，之后再介绍t-SNE。

Symmetric SNE

优化$p_{i \mid j}$和$q_{i \mid j}$的KL散度的一种替换思路是，使用联合概率分布来替换条件概率分布，即P是高维空间里各个点的联合概率分布，Q是低维空间下的，目标函数为：

$$C = KL(P \mid \mid Q) = \sum_i \sum_j p_{i,j} \log \frac{p_{ij}}{q_{ij}}$$

这里的$p_{ii}$,$q_{ii}$为0，我们将这种SNE称之为symmetric SNE(对称SNE)，因为他假设了对于任意$p_{ij} = p_{ji}, q_{ij} = q_{ji}$高维数据可视化，因此概率分布可以改写为：

$$p_{ij} = \frac{\exp(- \mid \mid x_i – x_j \mid \mid ^2 / 2\sigma^2)}{\sum_{k \neq l} \exp(- \mid \mid x_k-x_l \mid \mid ^2 / 2\sigma^2)}$$

$$q_{ij} = \frac{\exp(- \mid \mid y_i – y_j \mid \mid ^2)}{\sum_{k \neq l} \exp(- \mid \mid y_k-y_l \mid \mid ^2)}$$

这种表达方式，使得整体简洁了很多。但是会引入异常值的问题。比如$x_i$是异常值，那么$\mid \mid x_i – x_j \mid \mid ^2$会很大，对应的所有的$j$, $p_{ij}$都会很小(之前是仅在$x_i$下很小)，导致低维映射下的$y_i$对cost影响很小。为了解决这个问题，我们将联合概率分布定义修正为：$p_{ij} = \frac{p_{i \mid j} + p_{j \mid i}}{2}$，这保证了$\sum_j p_{ij} \gt \frac{1}{2n}$，使得每个点对于cost都会有一定的贡献。对称SNE的最大优点是梯度计算变得简单了，如下：

$$\frac{\delta C}{\delta y_i} = 4 \sum_j (p_{ij} – q_{ij})(y_i – y_j)$$

实验中，发现对称SNE能够产生和SNE一样好的结果，有时甚至略好一点。

Crowding问题

拥挤问题就是说各个簇聚集在一起，无法区分。比如有一种情况，高维度数据在降维到10维下，可以有很好的表达，但是降维到两维后无法得到可信映射，比如降维如10维中有11个点之间两两等距离的，在二维下就无法得到可信的映射结果(最多3个点)。 进一步的说明，假设一个以数据点$x_i$为中心，半径为r的m维球(三维空间就是球)，其体积是按$r^m$增长的，假设数据点是在m维球中均匀分布的，我们来看看其他数据点与$x_i$的距离随维度增大而产生的变化。

从上图可以看到，随着维度的增大，大部分数据点都聚集在m维球的表面附近，与点$x_i$的距离分布极不均衡。如果直接将这种距离关系保留到低维，就会出现拥挤问题。

Cook et al.(2007) 提出一种slight repulsion的方式，在基线概率分布(uniform background)中引入一个较小的混合因子$\rho$,这样$q_{ij}$就永远不会小于$\frac{2 \rho}{n(n-1)}$ (因为一共了n(n-1)个pairs)，这样在高维空间中比较远的两个点之间的$q_{ij}$总是会比$p_{ij}$大一点。这种称之为UNI-SNE，效果通常比标准的SNE要好。优化UNI-SNE的方法是先让$\rho$为0，使用标准的SNE优化，之后用模拟退火的方法的时候，再慢慢增加$\rho$. 直接优化UNI-SNE是不行的(即一开始$\rho$不为0)，因为距离较远的两个点基本是一样的$q_{ij}$(等于基线分布), 即使$p_{ij}$很大，一些距离变化很难在$q_{ij}$中产生作用。也就是说优化中刚开始距离较远的两个聚类点，后续就无法再把他们拉近了。

t-SNE

虽然Isomap，LLE和variants等数据降维和可视化方法，更适合展开单个连续的低维的manifold。但如果要准确的可视化样本间的相似度关系，如对于下图所示的S曲线（不同颜色的图像表示不同类别的数据），t-SNE表现更好。因为t-SNE主要是关注数据的局部结构。

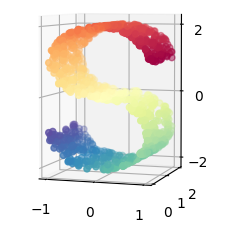
通过原始空间和嵌入空间的联合概率的Kullback-Leibler（KL）散度来评估可视化效果的好坏，也就是说用有关KL散度的函数作为loss函数，然后通过梯度下降最小化loss函数，最终获得收敛结果。注意，该loss不是凸函数，即具有不同初始值的多次运行将收敛于KL散度函数的局部最小值中，以致获得不同的结果。因此，尝试不同的随机数种子(Python中可以通过设置seed来获得不同的随机分布)有时候是有用的，并选择具有最低KL散度值的结果。

对称SNE实际上在高维度下另外一种减轻“拥挤问题”的方法：在高维空间下，在高维空间下我们使用高斯分布将距离转换为概率分布，在低维空间下，我们使用更加偏重长尾分布的方式来将距离转换为概率分布，使得高维度下中低等的距离在映射后能够有一个较大的距离。

我们对比一下高斯分布和t分布(如上图,code见probability/distribution.md), t分布受异常值影响更小，拟合结果更为合理，较好的捕获了数据的整体特征。

使用了t分布之后的q变化，如下：

$$q_{ij} = \frac{(1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}{\sum_{k \neq l} (1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}$$

此外，t分布是无限多个高斯分布的叠加，计算上不是指数的，会方便很多。优化的梯度如下：

$$\frac{\delta C}{\delta y_i} = 4 \sum_j(p_{ij}-q_{ij})(y_i-y_j)(1+ \mid \mid y_i-y_j \mid \mid ^2)^{-1}$$

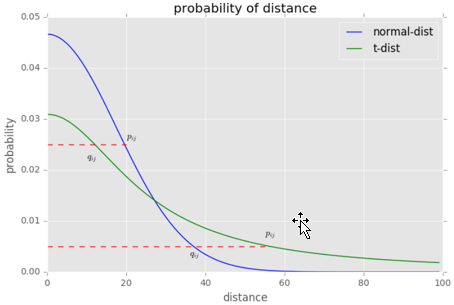
t-sne的有效性，也可以从上图中看到：横轴表示距离，纵轴表示相似度, 可以看到，对于较大相似度的点，t分布在低维空间中的距离需要稍小一点；而对于低相似度的点，t分布在低维空间中的距离需要更远。这恰好满足了我们的需求，即同一簇内的点(距离较近)聚合的更紧密，不同簇之间的点(距离较远)更加疏远。

总结一下，t-SNE的梯度更新有两大优势：

算法过程

算法详细过程如下：

结束结束

优化过程中可以尝试的两个trick:

优化的过程动态图如下：

不足

SKLearn中的t-SNE sklearn.manifold.TSNE

class sklearn.manifold.TSNE(n_components=2, perplexity=30.0, early_exaggeration=12.0, learning_rate=200.0, n_iter=1000, n_iter_without_progress=300, min_grad_norm=1e-07, metric=’euclidean’, init=’random’, verbose=0, random_state=None, method=’barnes_hut’, angle=0.5)

t-SNE的主要目的是高维数据的可视化。因此，当数据嵌入二维或三维时，效果最好。有时候优化KL散度可能有点棘手。有五个参数可以控制t-SNE的优化，即会影响最后的可视化质量：

参数说明：

属性：

方法：

注意事项：数据集在所有特征维度上的尺度应该相同。

为了可视化的目的（这是t-SNE的主要用处），强烈建议使用Barnes-Hut方法。method=”exact”时，传统的t-SNE方法尽管可以达到该算法的理论极限，效果更好，但受制于计算约束，只能对小数据集的可视化。

Barnes-Hut t-SNE主要是对传统t-SNE在速度上做了优化，是现在最流行的t-SNE方法，同时它与传统t-SNE还有一些不同：

sklearn.manifold.TSNE使用示例

1、输入4个3维的数据，然后通过t-SNE降维称2维的数据

import numpy as np
from sklearn.manifold import TSNE
X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
tsne = TSNE(n_components=2)
tsne.fit_transform(X)
print(tsne.embedding_)

2、S曲线的降维与可视化

from time import time
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter
from sklearn import manifold, datasets
from mpl_toolkits.mplot3d import Axes3D
# X是一个(1000, 3)的2维数据，color是一个(1000,)的1维数据
n_points = 1000
X, color = datasets.samples_generator.make_s_curve(n_points, random_state=0)
n_neighbors = 10
n_components = 2
# 创建了一个figure，标题为"Manifold Learning with 1000 points, 10 neighbors"
fig = plt.figure(figsize=(8, 8))

来源【首席数据官】，更多内容/合作请关注「辉声辉语」公众号，送10G营销资料！